编程日记3

题目1

【问题描述】

某个人写了n封不同的信及相应的n个不同的信封，他把这n封信都装错了信封，问都装错信封的装法有多少种？

【输入形式】

一个数

【输出形式】

结果

【样例输入】

9

【样例输出】

133496

【代码】

//错排：n封信放入n个信封，要求全部放错，共有多少种放法，记n个元素的错排总数为f(n)
//假设有n封信，第一封信可放在(2-n)的任一个信封里，共n-1种放法，设第一封信放在了第k个信封里，
//若此时第k封信放在了第1个信封里，则只要将剩下的n-2错排，即f(n-2)，
//若第k封信没有放在了第1个信封里，可将第1封信的位置看成是“第k个位置”，
//即将n-1封信错排，即为f(n-1)
//由递推可得,f(n)=(n-1)*(f(n-1)+f(n-2))
#include <iostream>
#include <iomanip>
#include <stdio.h>
using namespace std;

int fun(int n){
	if(n==1||n==0)
	{
	    return 0;
	}
	if(n==2){
		return 1;
	}
	else
	{
		return (n-1)*(fun(n-1)+fun(n-2));
	}
	
} 
int main(){
	
	int n;
	cin>>n;
	cout<<fun(n)<<endl;
	
	
}

题目2

【问题描述】

棋盘覆盖问题要求在2^k * 2^k 个方格组成的棋盘中，你给定任意一个特殊点，用一种方案实现是用包含3个方格的L型牌覆盖所有方格除该特殊点的棋盘实现全覆盖。

【输入形式】

Input the size and the x,y:8 7 6

【输出形式】

3 3 4 4 8 8 9 9

3 2 2 4 8 7 7 9

5 2 6 6 10 10 7 11

5 5 6 1 1 10 11 11

13 13 14 1 18 18 19 19

13 12 14 14 18 17 17 19

15 12 12 16 20 0 17 21

15 15 16 16 20 20 21 21

【样例输入】

Input the size and the x,y: 8 7 6

【样例输出】

3 3 4 4 8 8 9 9

3 2 2 4 8 7 7 9

5 2 6 6 10 10 7 11

5 5 6 1 1 10 11 11

13 13 14 1 18 18 19 19

13 12 14 14 18 17 17 19

15 12 12 16 20 0 17 21

15 15 16 16 20 20 21 21

【样例说明】

第一个数为棋盘的行列数，须为2的K次幂，后面两个数为特殊方格的行号和列好，小于等于第一个数，输出每个数字占4位

【代码】

#include<iostream>
#include<cmath>
#include<bits/stdc++.h>
using namespace std;
int tile = 1;
int Borad[100][100];
/**
 * tr : 棋盘左上角的行号，tc棋盘左上角的列号
 * dr : 特殊方格左上角的行号，dc特殊方格左上角的列号
 * size ：size = 2^k 棋盘规格为2^k*2^k
 */
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
    if(size==1)
        return;
    int t = tile++;
    int s = size / 2;
    if( dr< tr+s && dc< tc+s )//特殊方格在棋盘的左上角
    {
        ChessBoard(tr, tc, dr, dc, s);
    }
    else//特殊方格不在棋盘的左上角时；
    {
        Borad[tr + s-1][tc + s-1] = t;
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);

    }

    if( dr< tr+s && tc+s <=dc )//特殊方格在棋盘的右上角
    {
        ChessBoard(tr, tc + s, dr, dc, s);
    }
    else//特殊方格不在棋盘的右上角
    {
        Borad[tr + s-1][tc + s]=t;
        ChessBoard(tr, tc + s, tr + s-1, tc + s , s);
    }
    
    if( tr+s<= dr && dc < tc+s )//特殊方格在棋盘的左下角
    {
        ChessBoard(tr + s, tc, dr, dc, s);
    }
    else//特殊方格不在棋盘的左下角
    {
        Borad[tr+s][tc+s-1]=t;
        ChessBoard(tr + s, tc, tr+s, tc+s-1, s);
    }

    if( tr+s <= dr && tc+s <= dc )//特殊方格在棋盘的右下角
    {
        ChessBoard(tr + s, tc + s, dr, dc, s);
    }
    else//特殊方格不在棋盘的右下角
    {
        Borad[tr + s][tc + s]=t;
        ChessBoard(tr + s, tc + s, tr+s, tc+s, s);
    }

}
int main()
{
    cout << " Input the size and the x,y:";
    int k, x, y;
    cin >>k>>x>>y;
    y=y-1;
    x=x-1;
    int size = k;
    Borad[x][y] = 0;
    ChessBoard(0, 0, x, y, size);
    for (int i = 0; i < size;i++)
    {
        for (int j = 0; j < size;j++)
        {
            cout<<std::left<<setw(2)<<Borad[i][j]<<"  ";//数字向左靠齐 
        }
        cout << endl;
    }
        system("pause");

}

题目3

【问题描述】

递归法求x的n次方，n为整数，x为浮点数

【样例输入】

Input x,n:3.5 6

【样例输出】

The value is:1838.266

【样例说明】

一个空格隔开，输出小数点保留3位小数

【代码】

#include<iostream>
#include<iomanip>
using namespace std;
float UUU(float x,int N)//定义函数UUU 
{
        float temp;
        temp=1/x;
        if(N==1)
                return x;
        else if(N==0)
                return 1;
        else if(N>0)
                return x*UUU(x,N-1);//正数次幂使用递归
        else if(N<0)
                return 1*temp*UUU(x,N+1);//负数次幂乘以倒数
}
 
int main()
{
        float x;
        int N;
        float y;
       cout<<"Input x,n:";
        cin>>x>>N;
        y=UUU(x,N);
        cout<<endl<<"The value is:"<<fixed<<setprecision(3)<<y<<endl;
}

题目4

【问题描述】

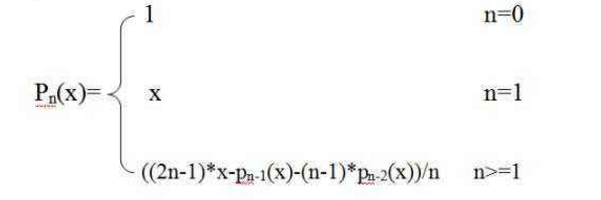
【输入形式】

please input n, x :3 1.5

【输出形式】

The Value of Legendre polynomials is：1.166667

【样例输入】

3 1.5

【样例输出】

The Value of Legendre polynomials is：1.166667

【样例说明】
输入的值之间用一个空格隔开

【代码】

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
double P(double x,double n){
	if(n==0)
	{
	    return 1;
	}
	if(n==1)
	{
		return x;
	}
	if(n>=1)
	{
		return ((2*n-1)*x-P(x,n-1)-(n-1)*P(x,n-2))/n;
	}
}

int main(){
	double x,n,z;
	cout<<"please input n, x :";
	cin>>n>>x;
	z=P(x,n);
	cout<<endl<<"The Value of Legendre polynomials is:"<<fixed<<setprecision(6)<<z;
}

代码可能略有不足，请大佬多多指教